mylab

Estruturas de dados (apontamentos)

Análise temporal:
Quanto tempo demora uma função?
Existem muitos fatores que fazem com que a resposta seja diversificada (dependo do hardware, do compilador, potencialmente variável)
O algoritmo não depende do hardware, e não depende da entrada
Mas o número de execuções de cada linha depende da entrada fornecida à função (dimensão do array, valores do array)

Tempo de execução vs Complexidade do algoritmo
A complexidade do algoritmo indica de que forma o seu tempo de execução varia com tamanho de entrada

Como representar a complexidade?
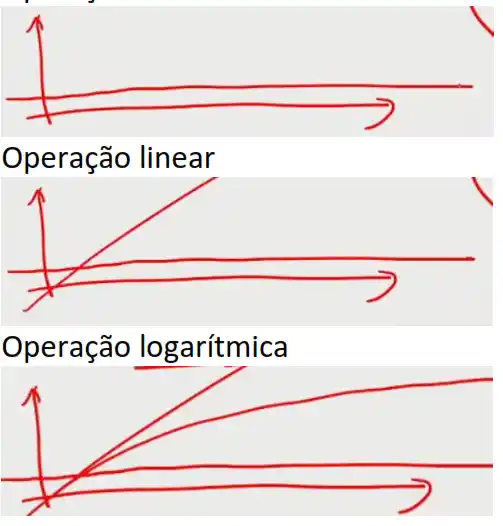
Com a notação de O-grande
O(n) – linear ou melhor, o tempo pode aumentar para o dobro ou pode ser menos do que isso
Ꝋ(n) – exatamente linear (Ꝋ, teta), o tempo vai realmente demorar o dobro se o tamanho do array passar o dobro.
Qualquer coisa Ꝋ(n) é obviamente O(n), qualquer coisa que é exatamente linear, é linear

Classes de complexidade:
• Ꝋ(1), O(1)
o Constante. É um algoritmo cujo tempo de execução é constante, ou tem tendência a manter-se contante quando a dimensão da entrada aumenta.
• Ꝋ(N), O(N)
o Linear.
• Ꝋ(N^2), Ꝋ(N^3),… O(N^2)
o Quadrática, cubica, .. Por exemplo: quadrático corresponde a um algoritmo quando a complexidade da entrada aumenta dez vezes o tempo de execução aumenta cem vezes, e se fosse cubico o tempo de execução aumentava mil vezes
• Ꝋ(log(N)), O(log(N))
o Logarítmica
• Ꝋ(N*log(N)), O(N*log(N))
o N-Log

O crescimento de funções:

Curva linear:
É melhor este algoritmo porque existe um ponto de dimensão de entrada a partir do qual o algoritmo linear é sempre melhor
Esse ponto existe sempre
Há-de existir um determinado valor de entrada a partir do qual o algoritmo linear vai ser sempre melhor do que o quadrático

Curva n Log n:
Também n Log n, vai ser mais baixo do que N^3 a partir de um determinado ponto
Curva quadrática:
Curva cúbica:

Assim para uma determinada dimensão e entrada “suficientemente grande” o algoritmo vai ser melhor.. o linear.

Existe a zona fácil: onde qualquer coisa funciona, processando poucos dados, indiferente a escolha do algoritmo

Os problemas relacionados com desempenho surgem, quando as dimensões dos dados processados aumentam.

A notação O-grande não indica um valor específico de tempo, mas vai indicar como a função cresce para valores suficientemente elevados da dimensão da entrada

Exemplo:
O tempo de execução de um algoritmo vem:
2n^3+20n
Temos um desempenho cubico, O(n^3)
E porque se ignora 20n, porque para valores grandes de n, os termos de maior valor como é o caso de n^3 é o termo que vão ser mais relevantes para o valor final

Situação do exemplo 1:
Se n=1
2*1^3 + 20*1, dá valores de 22
A maior parte do valor vem de 20n
Mas se n=2
2*2^3+20*2, dá valores de 48 (distribuição de 8+40)
Mas se n=3
(distribuição de 16+60)
Mas se n=10
(distribuição de 2000+200)
Assim desprezamos os valores de menor ordem, assim 2n^3+20n é uma função de O(n^3)
O 2 não acrescenta nada, pois dizer O(n) <=> o(2n)

Exemplo:
O tempo de execução de um algoritmo vem:
½ * n^2 + 200n – n log n
Temos um desempenho quadrático, O(n^2)

A notação de O-Grande, On, consegue abstrair-se do hardware,

Exemplo:
Qual é a complexidade de procurar o menor elemento num array de N elementos: Ꝋ(N),
porque é exatamente linear, eu não consigo saber o valor mais baixo sem ver todos os valores.
O(n) não está errado, mas não conseguimos ser melhor do que Ꝋ(N),
É exatamente linear

Exemplo:
Qual é a complexidade de procurar os dois pontos (x,y) mais próximos num plano num
conjunto de N pontos. Quando temos uma situação de soma de valores, de procurar,
1..2..3..4..5..6…. é quadrático, algoritmo é de complexidade quadrática, eu não sei se o último
par é o mais próximo, vou ter que ver tudo.
Existem N(n-1)/2
O tempo de execução de um algoritmo quadrático cresce muito depressa, para problemas a
sério não é possível usar algoritmos quadráticos, a sua ajuda é nula. A única situação é quando
o número de dados processados for estritamente limitado. Se a quantidade de dados poder
ser variável e aumentar existe zero algoritmos quadráticos com utilidade prática.
É exatamente quadrática,

Exemplo:
Verificar se num conjunto de N pontos há três que sejam colineares (que forem uma linha)
Existem N(n-1)(n-2) /6, complexidade cubica, polinómio de terceiro grau
O(n^3), não preciso de analisar todos os pontos, basta encontrar o primeiro, mas no pior caso
se não existir nenhum eu tenho que percorrer todos
É no pior caso cubica

(ED03 – Complexidade (Parte 2).pdf)
Só o tempo não é suficiente para analisar um algoritmo, para comparar algoritmos.
O empo é variável e difícil de definir de forma rigorosa
Usamos a analise de complexidade, que colocar os algoritmos em diferentes classes, como por
exemplo, constante, linear, quadrática, etc..
A notação para identificar a complexidade que usamos é O-Grande em que:

Algo linear, é O(N)
Algo quadrático, é O(N^2)
Em que N é o tamanho que estamos a resolver, tipicamente é a quantidade de dados que
estamos a processar

Exemplo:
N log N é Omega(N)?
Sabendo eu O(n) é linear ou melhor que é o mesmo que dizer que é <=
Ꝋ(N), representa o igual
Ómega(N), Maior ou igual, e quer dizer que é linear ou pior

Exemplo:
Considere que um algoritmo tem complexidade de ordem O(N). Quanto é que o tempo de
execução aumenta se o tamanho da entrada aumentar 10 vezes?
R:
O tempo de execução aumenta na mesma proporção da ordem que a complexidade
Algo quadrático que aumente 10x a dimensão de entrada, vai passar 100x mais
Algo quadrático que aumente 100x a dimensão de entrada, vai passar 10000x mais

#Logaritmos
Um logaritmo é o número de bits necessários para representar o número n
No logaritmo de base 2 indica: “o número de vezes que N deve ser dividido para atingir 1”

O(logBN) = O(log N) é o mesmo que O(5*N) = O(N)

Exemplo:
Dado um número X e um array A, devolver a posição de X em A ou uma indicação que X não
existe.

R:
Usando a Pesquisa Sequencial
Quantos valores temos que analisar numa pesquisa sem sucesso? Ꝋ(N)
De uma pesquisa com sucesso, no pior caso? Percorrer o array todo, Ꝋ(N)
De uma pesquisa com sucesso, no caso médio? .. o que é médio?..
A pesquisa sequencial é uma pesquisa linear

R:
Usando a Pesquisa Binária
Existe uma restrição: os dados têm que estar ordenados
O que interessa é eliminar uma % da pesquisa, tipicamente queremos eliminar 50%
Qual a complexidade de uma pesquisa falhada? É reduzirmos a pesquisa a 1 valor e esse valor
não é o que queremos procurar
E de uma pesquisa com sucesso, no pior caso? É ser o último valor
E de uma pesquisa com sucesso, no caso médio? É uma somatório de log..
E de uma pesquisa com sucesso, no melhor caso? O valor que quero é o que está no meio

O algoritmo de pesquisa Binária é mais eficiente do que o de Pesquisa Sequencial, se der para
ser aplicado

R:
Usando a Pesquisa Interpolada
O array está ordenado e E os valores estão uniformemente distribuídos

Qual é o pior caso? Os valores não estão uniformemente distribuídos, e podemos ter que
pesquisar todos

Qual é o caso médio? O(log log N)

Exemplo:
Qual a complexidade do seguinte algoritmo

Complexidade cubica, O(n^3), pois o terceiro for pode implicar percorrer todos os números
A maior parte do tempo vai ser para executar a linha 9

Podemos obter a versão 2:

A passa a ser de complexidade quadrática, O(N^2)

Podemos obter a versão 3:

A passa a ser de complexidade quadrática, O(N)

(ED04c- Genéricos.pdf)
Os métodos genéricos

Exemplo:
Pretende-se um método que imprime o conteúdo de um array:

E generalizando para qualquer tipo de dados:

Surge antes do valor de retorno <T>, tipo ou classe genérico

Exemplo:

Aqui o valor de retorno tem que ser da classe T
O tipo de valor que recebe é irrelevante
A lista <T> tem que aparecer antes do valor de retorno

Exemplo:
Podem também haver classes genéricas

E porque não usar o Object?
No Object não existe validação dos tipos
Nas funções get devolvo um object e terei que fazer um cast para o que lá está

É possível colocar restrições aos parâmetros formais.
Exemplo:

A restrição é feita usando extends Number, e talvez deixando em aberto a classe T pode
acontecer que uma arvore ou a class object não tenha o método doubleValue e dar erro/não
funciona

Assim adicionamos restrições aos parâmetros formais como por exemplo com o extends
Number (este Number pode também ser uma interface) e na classs Number existe o método
doubleValue

#Wildcards e restrições
As wildcards podem ser especificadas da seguinte forma:
Ou X extends Y, em que, X é igual a ou estende a classe Y (ou implementa interface Y), x é
derivado de Y
Ou X super Y, em que, Y é igual a ou estende a classe X (ou implementa interface X), Y é
derivado de X
Em algumas circunstâncias podemos:
X ou Y podem ser substituídos por ‘?’, o que significa “qualquer classe”, “qualquer coisa”

Exemplo:
public static <T,S> void f(par<T,S> p)
Pode ser escrito como
public static void f(par<?,?> p)

Exemplo:
public static <T, S extends T> void f(par<T,S> p)
Pode ser escrito como
public static <T> void f(par<T, ? extends T> p)
em que por exemplo T pode ser number, e S integer, já que integer é derivado de T

Exemplo:
public static <T> void f(par<T, ? extends T> p)
{
T p1 = p.getFirst(); //funciona
T p2 = p.getSecond(); //funciona porque existe o extends T
}
pois o que temos aqui é a=b, qual é a relação entre a e b?
têm que ser do mesmo tipo mas não necessariamente porque pode acontecer que
Figura a = new Reactangle();
Assim a = b, se a for do tipo T, tenho que garantir que seja qualquer classe que seja igual a T ou
derivada e isso faz-se com ? extends T

#Suporte de Polimorfismo com Wildcards
Exemplo:
public class Par <T,S> {
T primeiro;
S segundo;
public Par(T a, S b){
primeiro=a;
segundo=b;
}
public T getPrimeiro(){return primeiro;}
public S getSegundo(){return segundo;}
…
public void copia(Par<T,S> outroPar)
{
primeiro=outroPar.getPrimeiro();
Segundo=outroPar.getSegundo();

}
}

class Rect{
…
};
class Quad extends Rect{
…
}
public static void main(String args[])
{
Quad q1=new Quad(1), q2=new Quad(2);
Rect r1=new Rect(2,3), r2= new Rect (3,4);
Par<Quad,Rect> p1=new Par<>(q1,r1);
Par<Quad,Rect> p2=new Par<>(q2,r2);
p2.copia(p1); //ok
Par<Rect,Rect> p3=new Par<>(q1,r1);
Par<Rect,Rect> p4=new Par<>(q2,r2);
p3.copia(p4); //ok
p3.copia(p1); // erro de compilação:
//Par<Quad,Rect> não pode ser usado
// no lugar de Par<Rect,Rect>
}

Não compila pela forma como foi definido o parâmetro
A função copia está definida de forma demasiado restritiva pois não foram usados wildcards

Outra versão do copia:
public void copia
(Par<? extends T,? extends S> outroPar)
{
primeiro=outroPar.getPrimeiro();
Segundo=outroPar.getSegundo();
}

Desta forma quando se faz
primeiro=outroPar.getPrimeiro();
se a=b, ou pode ser qualquer coisa que seja derivado de T -> ? extends S
o primeiro parâmetro seja qualquer coisa T ou derivado de T -> ? extends T

estas duas restrições
<? extends T,? extends S>
vão permitir que o código assim compile
permitem uma maior gama de classes

E a comparação entre coisas?
Se forem tipos básicos de dados, por exemplo a > b vai funcionar
Mas e se forem objetos?
É usado o interface comparable

Exemplo:
Class Figura com,

class Figura implements Comparable<Figura>{
int compareTo(Figura f){…}
}
Class Rect extends Figura{…}
…

Rect r=new Rect(2,3), q=new Rect(3,4);
r.compareTo(q);

Tem que se implementar a interface Comparable
E assim Figura pode ser comparada com outras figuras
E tenho que implementar o método compareTo
<, se se for menor,
0 se for igual
>0, se for maior
E não esquecer que Rect extends Figura

E isto é válido que o Rect é uma figura, e assim todas as figuras são comparáveis entre si, até
podem ser rect ou círculos

Exemplo:
Temos,
class Figura implements Comparable<Figura>{
int compareTo(Figura f){…}
}
<T> int compara (Comparable<T> a , Tb ){
return a.compareTo(b);
}
Rect r=new Rect(2,3), q=new Rect(3,4);
r.compareTo(q);
Compara(r,q); //funciona? Não..

O retângulo é comparable com rect?
Não, figura é comparable com figura
Só funciona se o r e o q forem figuras

Será que funciona se usarmos
Comparable<? extends T> T
Não é verdade! Errado.. porque não se vai comparar círculos com retangulos

E se for:
Comparable<Object> T
Sim funciona.

Assim o que está correto é comparar com uma classe qualquer, que pode ser T ou Super
ficando assim:
Comparable<? Super T> T

Exemplo:
Temos,
class Figura implements Comparable<Figura>{
int compareTo(Figura f){…}

}
<T> int compara (Comparable<? super T> a , Tb ){
return a.compareTo(b);
}
Rect r=new Rect(2,3), q=new Rect(3,4);
r.compareTo(q);
Compara(r,q); //funciona?

Análise do uso do super:
R é um rectangulo, Rect
Q é um rectangulo, Rect
R tem que ser comparable com um tipo qualquer que é Rect ou que está acima de Rect
Isso verifica-se porque Rect é comparable com Figura, que é um tipo que está acima de Rect

Super:
Aplica-se em situações em que queremos garantir que o tipo que usamos pode receber do tipo
original

Em qualquer situação em que existam genéricos, por exemplo:
<T, S extends Comparable <T>> void f() não é isto que se pretende escrever mas sim
<T, S extends Comparable <? Super T>> void f()
A intenção é a de fazer a comparação com T ou classe ou acima dela

Exemplo:
<T> void find(List<? super T> l, T t)
{
..
l.add(t);
}
Faz sentido? Sim já o seguinte não faz
<T> void find(List<T> l, T t)
{
..
l.add(t);
}
Já que só conseguia procurar por exemplo uma string numa lista de strings

Com o uso do super eu olho para cima, isto é, posso colocar os Rect numa lista de Figuras

#Limitaçãoes dos genéricos
Os genéricos só existem durante a compilação

Exemplo:
Como definir uma classe ParComparável, sabendo que esta representa um Par cujos
elementos são comparáveis. A classe ParComparável deve por sua vez ser também
comparável: a comparação deve ser decidida através da comparação dos dois primeiros
elementos de cada par, desempatando com a comparação dos segundos.

Parte 1:
uma classe ParComparável, sabendo que esta representa um Par cujos elementos são
comparáveis

public class ParComparavel <S extends Comparable<? super S>,
T extends Comparable<? super T>>
extends Par<S,T>
{…}

Parte 2:
A classe ParComparável deve por sua vez ser também comparável
public class ParComparavel <S extends Comparable<? Super S>,
T extends Comparable<? Super T>>
extends Par<S,T>
implements Comparable<ParComparavel<? extends S,? extends T>>
{…}

Parte 3:
a comparação deve ser decidida através da comparação dos dois primeiros elementos de cada
par, desempatando com a comparação dos segundos
class ParComparável …{
…
int compareTo(ParComparavel<? extends S,? extends T> p)
{
int compPrimeiro= p.getPrimeiro().compareTo(getPrimeiro());
if(compPrimeiro==0)
return p.getSegundo(getSegundo());
else
return compPrimeiro;
}
…
}

ED05-iteradores.pdf
#iteradores
Server para isolar as estruturas de dados dos algoritmos que usam as estruturas de dados
Os iteradores são objetos utilizados para percorrer estruturas de dados

Para se implementar por exemplo um iterador:
public interface Iterator<E>{
boolean hasNext();
E next() ; // gera excepção caso não exista
}
Em que E é o tipo de objeto que estamos a percorrer
E dois métodos importantes: hasNext e o next
Em que o
hasNext
devolve verdadeiro ou falso se existem mais valores para percorrer e o next avança para o próximo valor E devolve o próximo valor

Exemplo:
public class Par <T> implements Iterable<T>
{
T p1,p2;
Iterator<T> iterator(){

return new IteratorPar<T>(this);
}
…
};

É importante:
implements Iterable<T>
pois é uma classe iterável, que nos fornece um iterador para percorrer os valores que lá tem
dentro
e com Iterator<T> iterator(){
que é o método que devolve o iterador para objetos do tipo T

e
public class IteratorPar<T> implements Iterator<T>{
int counter=0;
Par<T> par;
IteratorPar( Par<T> p){par=p;}
Boolean hasNext() {return counter!=2;}
T next(){
switch(counter)
{
case 0: counter++; return par.p1;
case 1: counter++; return par.p2;
default: throw new NoSuchElementException();
};
}
}

Iterator diferente de Iterable, cuidado
E na classe IteratorPar tem implementado os métodos
hasNext e next

Com algoritmos também se pode:
public <T> boolean procura(Iterable<T> m, T o){
Iterator<T> it=m.iterator();
boolean proximo=it.hasNext();
while(proximo){
if(it.next()==0) // compara referência, não conteúdo
return true;
proximo=it.hasNext();
}
return false;
}

Inclui-se o Iterable
Em
public <T> boolean procura(Iterable<T> m, T o){
chamar a função iterator para se ir buscar o iterador
Iterator<T> it=m.iterator();
Depois chamar hasNext para saber se existe o próximo valor
boolean proximo=it.hasNext();
chamar o next para devolver o valor se existir

if(it.next()==0)
e continuar a procurar o próximo valor
proximo=it.hasNext();

este método funcionar com a classe Par
Par<Integer> p = …
Procurar (p,x);
Ou funciona se tiver uma lista
List<Integer> l = ..
Procurar(l,x)

Nos ciclos for abreviados
for(integer i: l)
{
…
}
for(integer: p)
{
…
}

#Iteradores e Excepções
Os iteradores podem/devem gerar as seguintes excepções:
– NoSuchElementException – Tentativa de acesso a um elemento que não existe
– UnsupportedOperationException – A operação (p.ex: remoção) não é suportada.
Existem também o método remove, mas que não faz sentido para este tipo de dados
Mas,
O método remove, remove um valor
O valor que vai ser removido não é o que é apontado pelo iterador já que o iterador aponta
para o meio de dois números
O método remove, remove o último valor devolvido pelo next
Exemplo:
Temos uma lista l
Uso um iterador:
It = l.iterator();
E faz-se um remove
It.remove();
Que valor é que remove?
Como não existe o next, porque o next nunca devolveu um valor, não vai remover nada e cria a
excepção IllegalStateException

Exemplo: Se quero remover o valor
Uso um iterador:
It = l.iterator();
Faz o next
It.next() //para devolver neste caso o primeiro valor
E faz-se um remove
It.remove();

Exemplo: e se surgir o seguinte:
It = l.iterator();
It.next()

It.remove();
It.remove();

O valor que ele vai remover, não é nada, porque não houve next, surge então o
IllegalStateException. Apos o primeiro remove a seguir ao next não está lá nada.

– IllegalStateException – Tentativa de remoção sem avançar para primeiro elemento ou
tentativa de remover o mesmo elemento mais do que uma vez.
– ConcurrentModificationException – Quando se tenta usar um iterador inválido. Um iterador
é inválido quando a colecção foi alterada externamente (através de um outro iterador, por
exemplo).

Exemplo:
Valores guardados 1 2 3
next() devolve 1
next() devolve 2
remove() apaga 2
next() devolve 3

faltou ver o ConcurrentModificationException

#API de Colecções
Todas as estruturas de dados implementam a interface Collection<T>.
Inserção/Remoção: add, addAll, remove, removeAll, retainAll, clear.
Conversão para array: toArray
Suporte para iteradores: iterator
Informação e pesquisa: isEmpty, size, contains, containsAll

todas as implementações de Collection deverão possuir os seguintes construtores:
– Construtor sem parâmetros
– Construtor que cria uma colecção que referencia os mesmos elementos que outra colecção

Exemplo:
class Pacote <X> implements Collection<X>
{
Pacote(){
//cria colecção vazia;
…
}

Pacote(Collection<? extends X> c){
//cria uma colecção que referencia
//os mesmos elementos que c
…
}
…
}

#Tipos de Colecções – List
Implementações de List:
LinkedList
ArrayList (ou Vector)

Têm métodos para as posições dos objetos:
indexOf
set
get

e iteradores bidirecional:
listIteraor() e listIterador(int index)

e o ListIterator tem os métodos:
hasNext
next
add //insere elemento na lista
hasPrevious
nextIndex//retorna o índice do próximo elemento
previous //retorna o elemento anterior
set //modifica o valor que foi devolvido

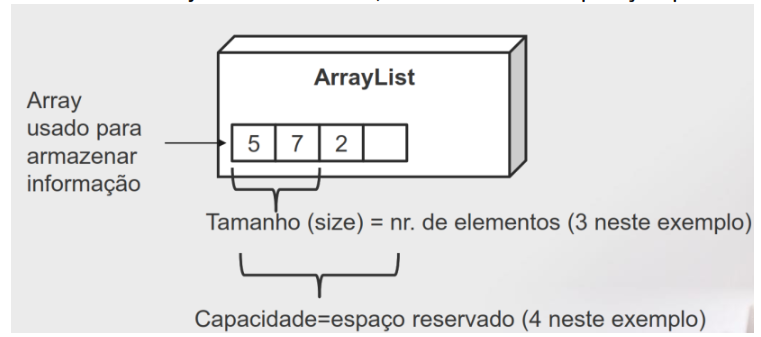
# Operações sobre ArrayLists
A ordem dos objetos é relevante, onde existe uma posição para cada objeto

Conceitos importantes: tamanho e capacidade

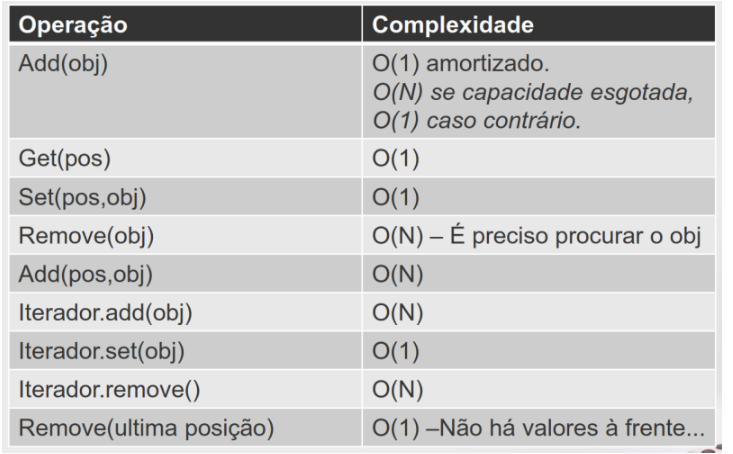
Qual é a complexidade das funções sobre as ArrayLists?
Qual a melhor estrutura de dados adequada para um determinado cenário?

Acrescentar um valor
Só funciona se a capacidade for maior do que o tamanho, a inserção é feita em tempo
constante O(1)
Exemplo:
a[size] = v;
size++;

e se não existir espaço livre?
Recriar o novo espaço maior, O(1)
Copiar todo o conteúdo para o novo espaço, o(N) (vou demorar o dobro do tempo a copiar,
demora tempo proporcional a N)
E adicionar o novo valor

A complexidade de add(N) vem:
O(1), operação de tempo constante, capacidade > tamanho (size) ou tamanho < capacidade,
O(N), operação de tempo linear, capacidade = tamanho (size)

E se tiver que realocar, qual é novo espaço que se deve alocar?

Acrescentar mais um valor na capacidade fica com complexidade O(N^2) que é muito mau.
O número de células a aumentar não pode ser constante, assim se o valor atual, N, for 10 eu
por exemplo devo aumentar para 2x mais, para 20… pois desta forma atinge-se
comportamento constante amortizado.
Eu tenho um pico quando crio o novo espaço e copio a primeira vez, mas depois eu sei que a
seguir não vou demorar tanto tempo, ele vai ser amortizado, as próximas inserções vão ser
eficientes.
Se eu inserir n valores o tempo vai ser O(N),
A inserção de 1 é O(1) e vamos ter o custo de O(1) amortizado (os tempos eficientes diuense)
Se inserirmos um numero, suficientemente grande de números da valores, a operação é de
tempo O(1) amortizado
Na pior das situações o último valor a inserir é o valor que provoca o aumenta da capacidade,
e se isso acontece vou ter mais o dobro do espaço, e esse espaço não vai ser usado e é um
custo

Exemplo:
Se eu precisar de uma estrutura em que vou adicionando valores, se calhar um array list é uma
estrutura boa, porque o desempenho vai ser de O(1) amortizado para uma utilização normal,
em termos de desempenho natural, usando adds

Complexidade de aceder a um valor de um arrayList:
Tem tempo Constante, vou para a posição usando o get

Complexidade de remover um valor de um arrayList:
Remover um valor de uma posição,
Terei que copiar os seguintes para as posições anteriores
//isto é operação de tempo linear, O(N)
E decrementar o size
E,
A pior posição para remover num arrayList é a primeira
A melhor posição para remover num arrayList é a ultima

Exemplo:
for(i=0; i <N; i++) //N vezes
if(l.get(i) = =0){ //O(1), linear
l.remove(i); //O(N)
i–;
}
}
O tempo deste código é O(N^2), o que é mau..

Mas existem variações no remove, por exemplo se eu for remover o último da posição do
array, vamos ter que percorrer o array todo para procurar o objecto a remover
A operação remove object vai demorar sempre um tempo linear

Uma forma melhorada do remove é começar a procurar do fim para o inicio, é uma ligeira
otimização para tentar a manter o desempenho constante.

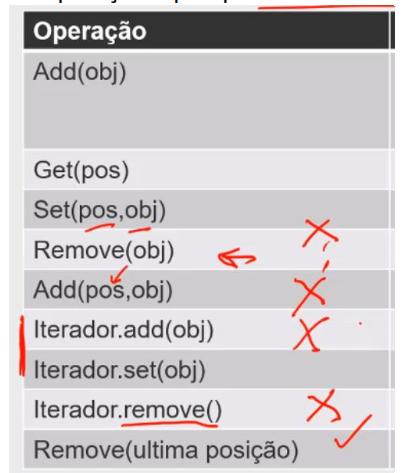
Situações no arrayList:

O(1), tempo constante
O(N), pelo menos é linear

As operações que quero evitar no arrayList são:

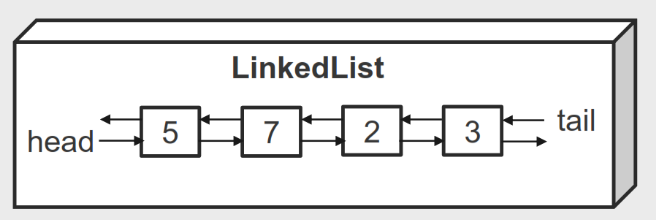
# Operações sobre LinkedLists
Usando listas duplamente ligadas

Qual a complexidade do get para aceder a uma posição aleatória?
Tenho que começar de uma das pontas e chegar à posição pretendida, complexidade linear,
O(N)

Qual a complexidade do adicionar um novo valor?
Tempo constante, não interessa o tamanho da lista, O(1) verdadeiro e não amortizado

Qual a complexidade do adicionar um novo valor no inico?
Tempo constante, não interessa o tamanho da lista, O(1) verdadeiro e não amortizado

Qual a complexidade do adicionar um novo valor no meio?
Tempo linear, tenho que ir até à posição onde quero inserir, não é melhor do que um arrayList

Exemplo:
for(i=0; i <N; i++){ //N vezes
print(l.get(i)); //O(N)
}
Demora então N^2

Situações na LinkedList:

Usando iteradores neste caso é sempre tempo constante, O(1)

Exemplo:
for(i=0; i <N; i++){ //N vezes

if(i.get(i) ==0) //O(N)

l.remove(i) //O(N)
}
Demora então N^2.. comportamento quadrático
Não esquecer que O(N) +O(N) = 2*O(N^2) mas que fica O(N^2)

Exemplo:
while(it.hasNext){ //percorrer os valores todos

if(i.next(i) ==0) //O(1) //operação que demora tempo constante

l.remove(i) //O(1) //operação que demora tempo constante
}
Comportamento linear

Quando se faz uma operação por exemplo de procurar algo na linkedList, estou a fazer O(N),
contudo com esta operação o iterador já lá fica “nessa posição” e assim sendo quando voltar a
fazer outra operação o iterador “já pode lá estar”

Se eu tiver um objecto que recebe um objeto do tipo List, por exemplo:
List<T> L
Não sabemos o que temos, pode ser um arrayList ou pode ser um linkedList, devemos usar o
iterador, pois não sabemos que tipo de lista que vamos receber

Faltou: especialização do interface Collection Set, especialização do interface Collection
Queue, e a hierarquia de colecções Map,

[aula 05]
ED07-Arvores Binarias.pdf
#Árvores Binárias

Nas Árvores Binárias temos, zero um ou dois descendentes em cada nó

Operações básicas nas Árvores Binárias:
getNumeroNodos()
getAltura()
imprimePreOrdem()
imprimePosOrdem()
imprimeEmOrdem()

existem três formas básicas de percorrer a árvore: PreOrdem, PosOrdem e EmOrdem

A recursividade e o número de nodos de uma árvore com raiz

As funções recursivas têm que ter:
1) Condição de paragem (encontrar a situação em que encontramos o valor a devolver)
2) Construir a função como se ela estivesse a funcionar (“fazer função como se já funcionasse”)

Uma arvore vazia tem zero nós, se o nodo R (raiz) for Null então o número de nós é zero.
O número de nodos de uma árvore com raiz R é dado pela soma do número de nodos na
subárvore esquerda com o número de nodos na subarvore direita mais um (a própria raiz)!

Exemplo:
int numerNodos(Nodo raiz){

if(raiz == null) return 0; //condição de paragem

return 1+numeroNodos(raiz.esquerda)+numeroNodos(raiz.direita);
}

ED (cálculo) <- Percorrer os descendentes da raiz e depois faz algo (determinar número de
nodos) à raiz
Em pós-ordem: primeiro vou percorrer as subárvores do lado esquerdo e do lado direito e
depois é que vou ao nodo da raiz

Exemplo:
Calcular o número de nodos da subárvore da raiz, sem saber o número de nodos da arvore
Tenho que saber sempre o número de nodos

Exemplo: copiar uma arvore em pre-ordem, faz sentido porque preciso de ancorar anyes de
fazer a copia das subárvores

void copia(Nodo R){
if(r==NULL) return null;
Nodo novo= new Nodo(r.valor);
novo.esq = copia(r.esq);
novo.dir= copia(r.dir);
return novo;
}

#Travessia de Árvore
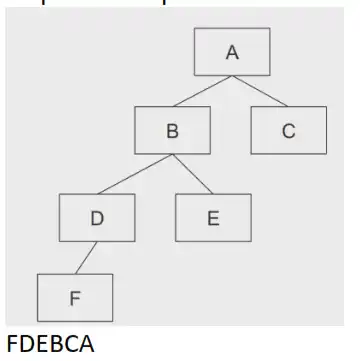
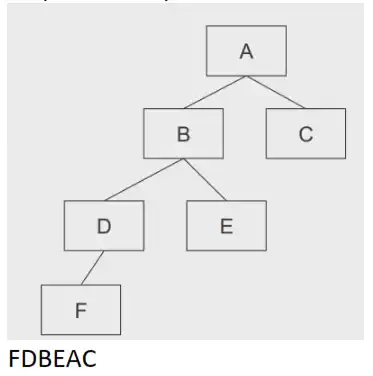
Sequencia de percorrer a arvore em preordem, visito o nodo, depois o lado esquerdo e depois o lado direito

Sequencia de percorrer a arvore em posordem, lado esquerdo e depois o lado direito e nodo

Sequencia de percorrer a arvore em ordem, lado esquerdo, nodo, e depois o lado direito

#Aplicações de Árvores Binárias

Servem para representar expressões:

Exemplo:
Nodos internos representam as operações
As folhas os valores

void imprimir(Nodo n){
if(nodo== null) return;
imprimir(n.esq)
print(n.valor)
imprmiri(n.dirt)
}

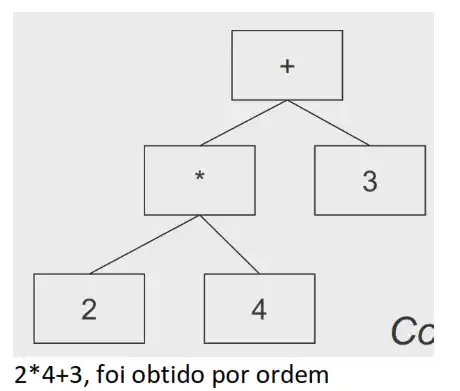
Mas para calcular é obtido por posordem, por exemplo:
Integer CalculaValor(){
if (esquerda==null)&&(direita==null)
return Integer.valueOf(valor);
int valEsq=esquerda.CalculaValor().intValue();
int valDir=0;
if(direita!=null)
direita=direita.CalculaValor().intValue();
if (valor.equals(“+”))
return valDir+ValEsq;
if (valor.equals(“*”))
return valDir*ValEsq;
if (valor.equals(“-”))
return valDir-ValEsq;

…

A construção de uma árvore é mais simples se tivermos a expressão representada em pos-fix.
Notação pos-fix, os operadores estão depois dos argumentos e não entre eles (não se usam
parêntesis)
Notação in-fix, os operadores estão entre argumentos (podem usar-se parêntesis)
Exemplo:
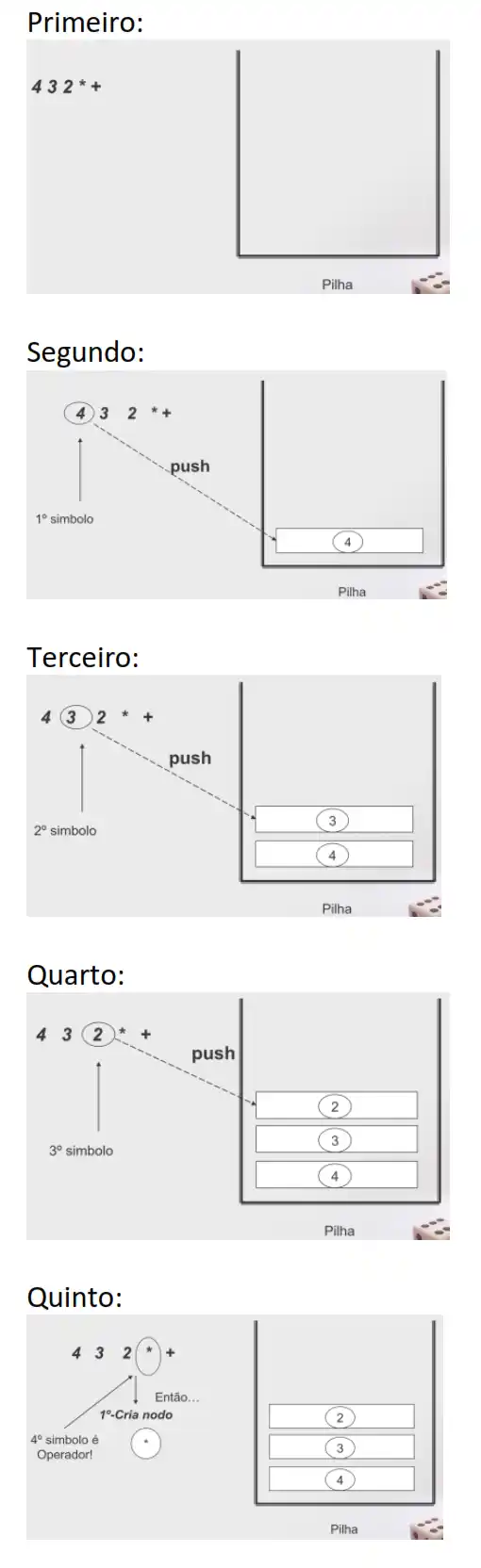
4+3*2 (infix) é equivalente a 4 3 2 * + (postfix)

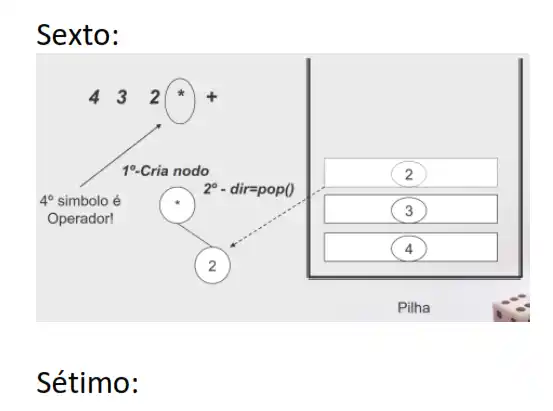
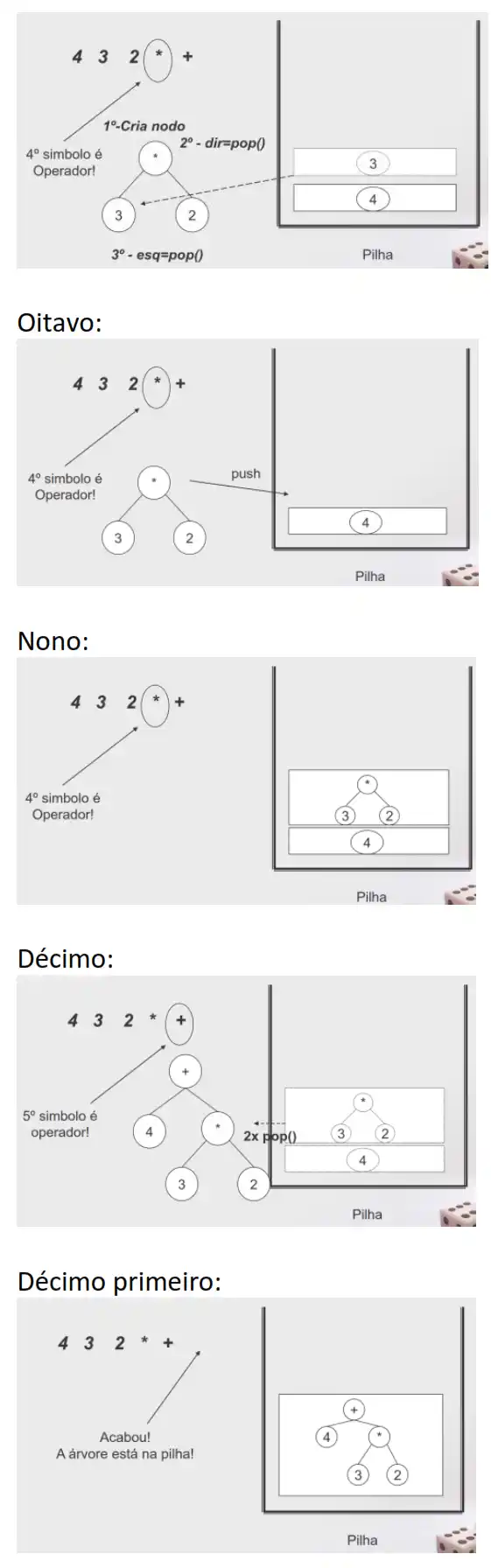
Exemplo: converter post-fix para árvore de 4 3 2 * +

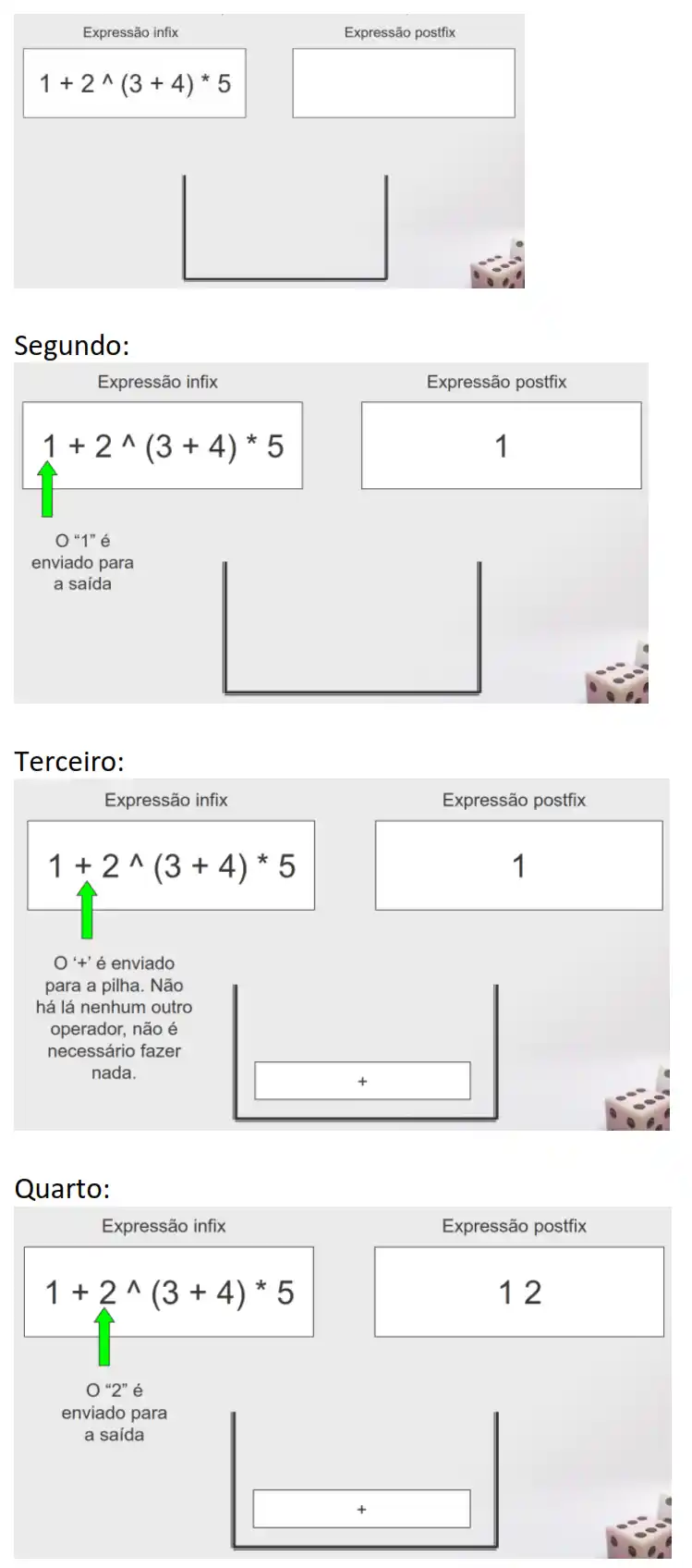
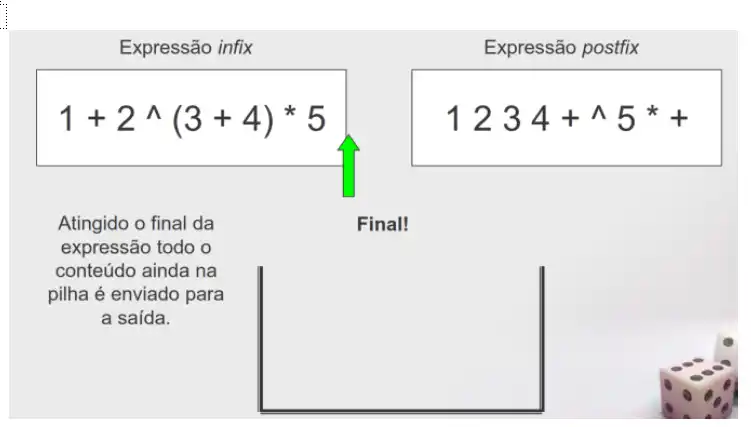
Exemplo: converter de infix para postfix, sabendo que 2 (infix) é equivalente a 4 3 2 * +
(postfix)

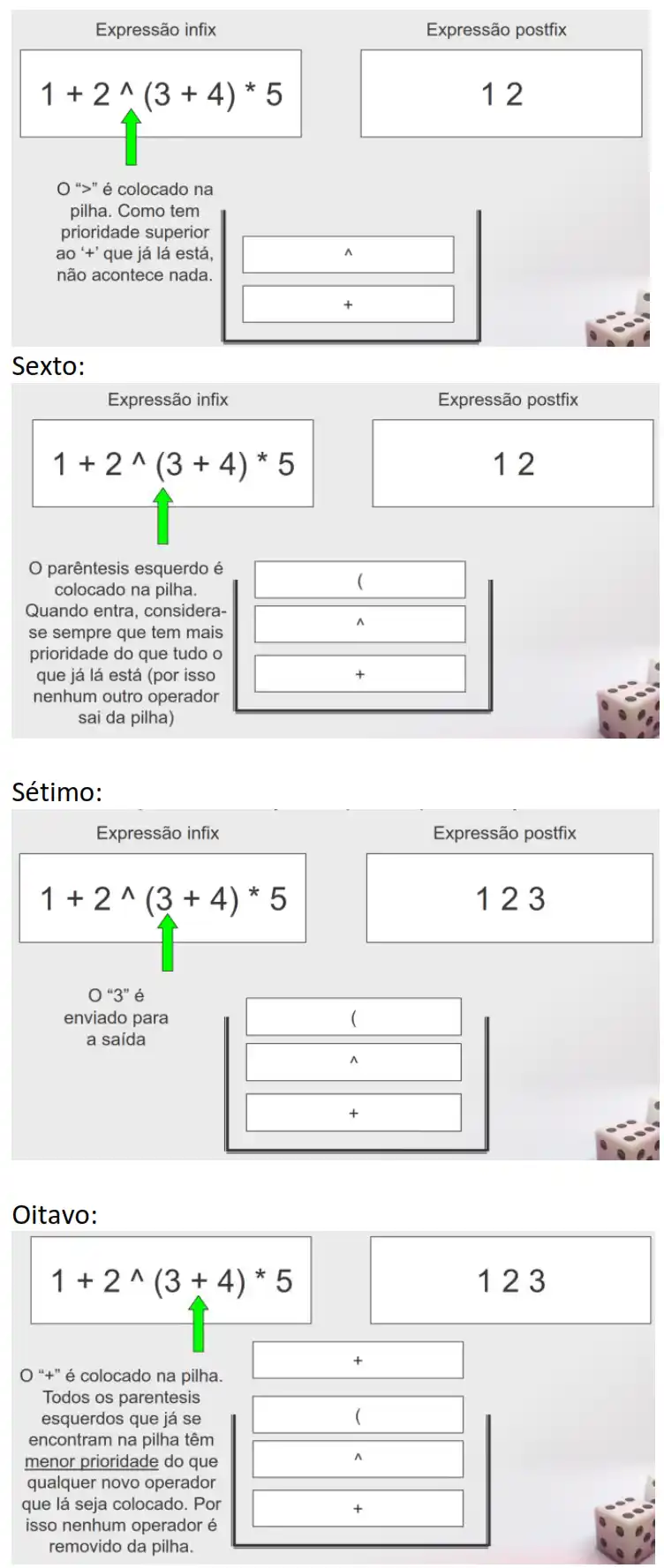
Primeiro:

Quinto:

Nona:

Decima terceira:

As árvores podem ser usadas na compressão de dados, árvore de Huffman
Não existe uma só arvore, podem ter codificações diferentes

Exemplo:
Texto a comprimir:
“banana ananaz”

Em que posso codificar:
‘a’ (6 ocorrências) =1
‘n’ (4 ocorrências)=00
‘z’ (1 ocorrência) =0111
‘b’ (1 ocorrência) =0110
‘ ‘ (1 ocorrência)=010

Texto recodificado:
“0110100100101010010010111”

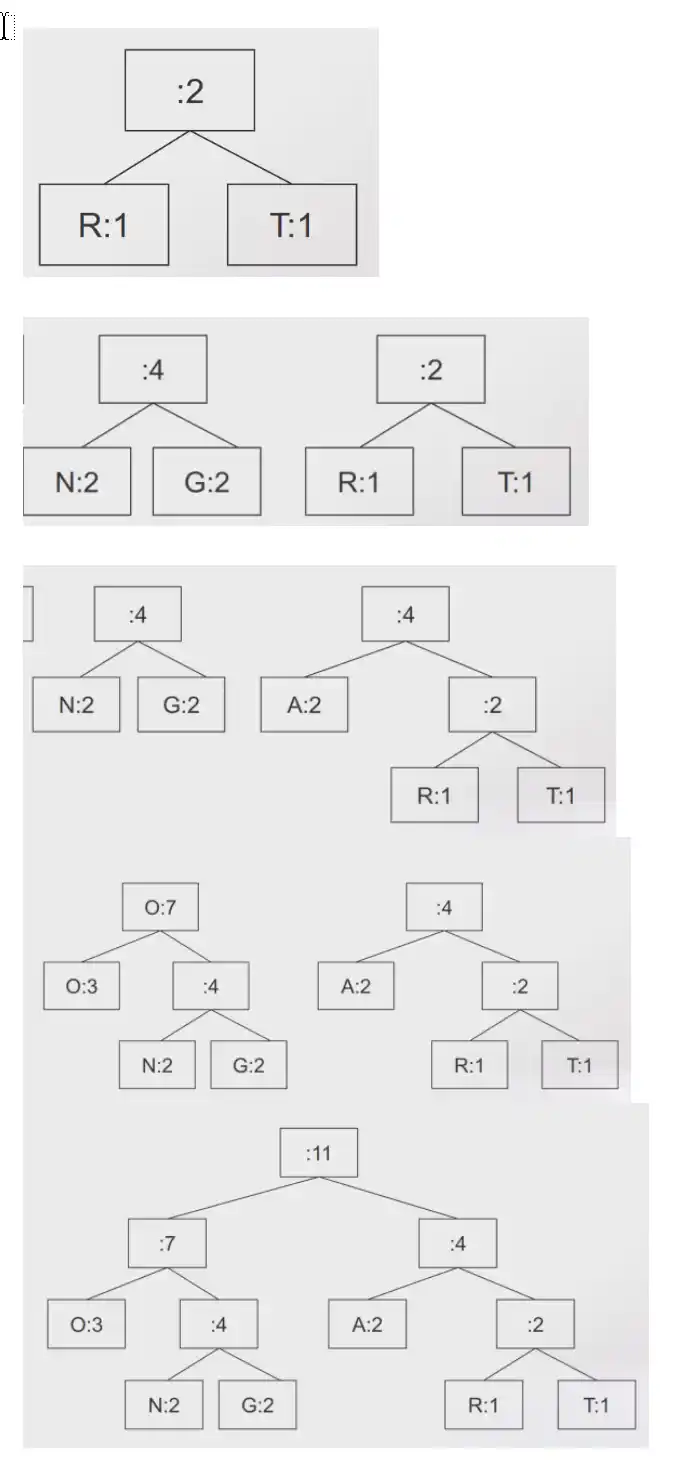
A árvore de Huffman é construída de baixo para cima, e agregamos subárvores de acordo com
a frequência dos símbolos que a subárvore representa.
E quando se escolhe que duas subárvores que devemos juntar numa nova arvore, vamos
escolher as duas subárvores que tenham menos símbolos. Os empates são resolvidos ao calhas

Exemplo:
ORANGOTANGO

1) efetuar o calculo a frequência das letras
O 3
A 2
N 2
G 2
R 1
T 1

2) Agrupam-se dois dos elementos com menor frequência numa única árvore

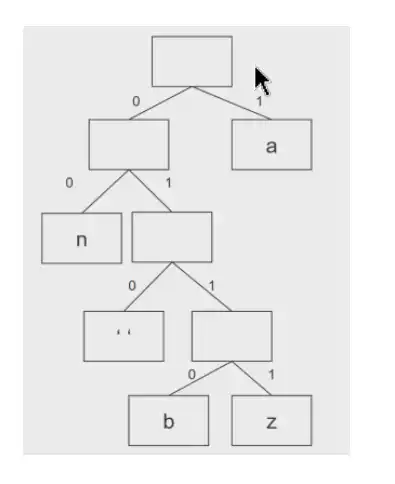
As folhas da árvore vão corresponder sempre a símbolos do texto
A codificação é dado por 0 (esquerda) e 1 (direita)

#Arvores binárias de pesquisa
São usadas para criar estrutura de dados que tem tempos de inserção e pesquisa tempo
logarítmico, porque a altura de uma árvore de N nodos está relacionado com Log de N

É uma arvore binária tem como critério inicial que é:
propriedade de ordem,
Todos os nodos na sub-árvore esquerda de um nodo raiz são menores do que a essa raiz
Todos os nodos na sub-árvore direita de um nodo raiz são maiores do que essa raiz.
E não existem valores iguais

E os valores iguais?
Não existe sítio para os colocar
Se for necessário: ter um contador no nodo, ou ter uma estrutura auxiliar no nodo que conta

Travessia de árvore equilibrada:
Caso uma árvore de pesquisa equilibrada seja percorrida em ordem, os elementos são
visitados por ordem crescente.

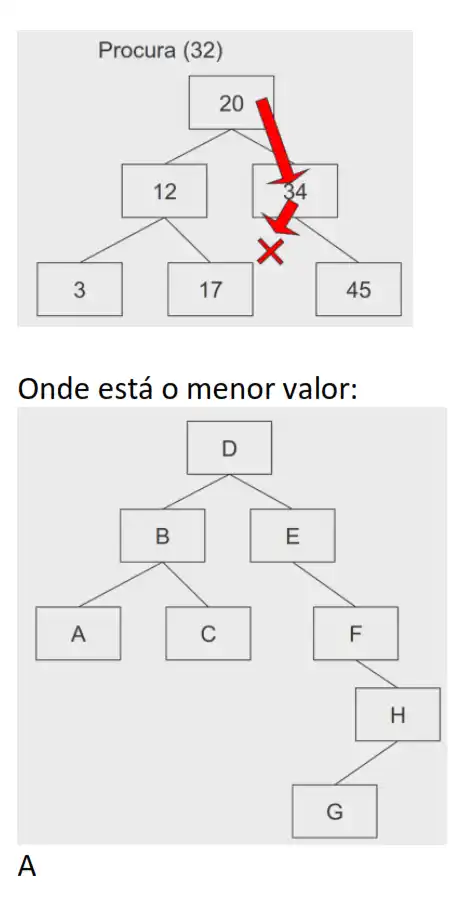
Como pesquisar um valor em árvores binárias equilibradas:
Para procurar o valor X numa árvore binária com raiz R, verificasse R contém X. Caso isso não
aconteça, procura-se na sub-árvore esquerda ou direita conforme o elemento a procurar seja
menor ou maior, respectivamente, do que o valor da raiz.

Exemplo:

Algoritmo de pesquisa do Elemento Mínimo:
private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t )
{
if (t==null)
return null;
if(t.left==null)
return t;
else
return findMin(t.left);
}

Algoritmo de pesquisa:
private BinaryNode<AnyType> find( AnyType x, BinaryNode<AnyType> t )
{
if( t != null )
{
if( x.compareTo( t.element ) < 0 )
return find(x,t.left);
else
if( x.compareTo( t.element ) > 0 )
return find(x,t.right);
else
return t;
// Encontrado
//(Resultado menos provável testado em último lugar)
}
return null;
}

[aula06]
# Árvores de Pesquisa Binárias: a Inserção

Caso a árvore esteja vazia, cria uma raiz nova.
Caso contrário:
Se for igual à raiz, gera excepção.
Se for maior do que a raiz, insere na subárvore direita
Se for menor do que a raiz, insere na subárvore esquerda.

protected BinaryNode<AnyType> insert ( AnyType x, BinaryNode<AnyType> t )
{
if( t == null )
t = new BinaryNode<AnyType>( x ); //condição de saida
else
if( x.compareTo( t.element ) < 0 )
t.left = insert( x, t.left );
else if( x.compareTo( t.element ) > 0 )
t.right = insert( x, t.right );
else
throw new DuplicateItemException( x.toString( ) ); // Duplicado, condição de
saida
return t; //nova raiz desta sub-árvore
}

“Nodo, é a nova raiz da arvores depois da inserção”

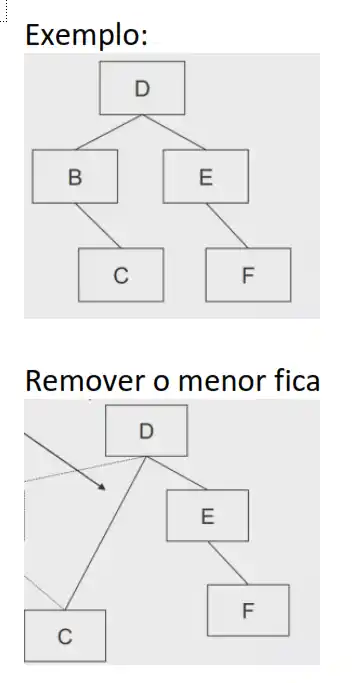
# Árvores de Pesquisa Binárias: a remoção
O caso simples: remover o menor valor de uma subárvore

A função para remover o mínimo pode alterar a raiz da arvore?
Sim, se o menor for a raiz, assim a função devolve um Nodo e não Void, e vai ser usada a
recursividade

public void removeMin(){
root=removeMin(root);
}

private BinaryNode<AnyType> removeMin( BinaryNode<AnyType>t)
{
if( t == null )
throw new ItemNotFoundException( );
else
if( t.left != null )
{
t.left = removeMin( t.left );
return t;
}
else
return t.right;
}

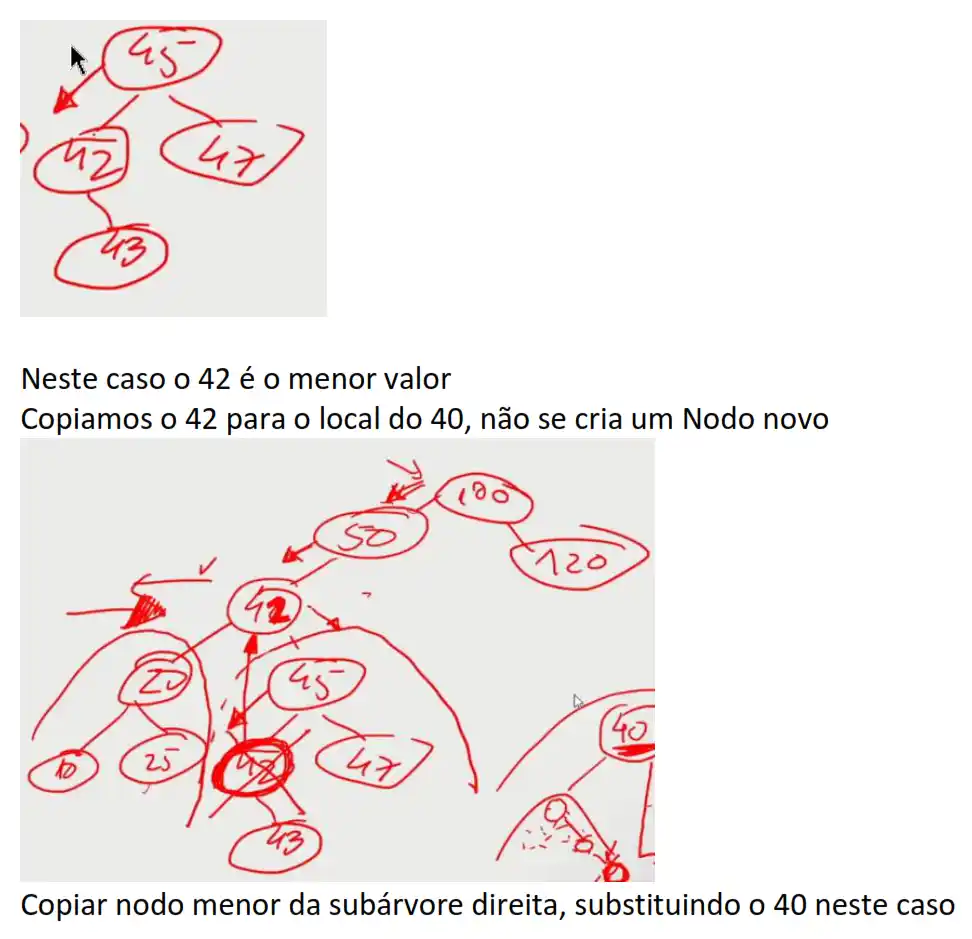
Copiar nodo menor da subárvore direita, substituindo o 40 neste caso

O algoritmo:
protected BinaryNode<AnyType> remove( AnyType x, BinaryNode<AnyType> t )
{
if( t == null )
throw new ItemNotFoundException( x.toString( ) );
if( x.compareTo( t.element ) < 0 )
t.left = remove( x, t.left );
else if( x.compareTo( t.element ) > 0 )
t.right = remove( x, t.right );
else
if( t.left != null && t.right != null ) // Dois descendentes
{
t.element = findMin( t.right ).element;
t.right = removeMin( t.right );
}
else
t = ( t.left != null ) ? t.left : t.right; // Um só descendente
return t;
}

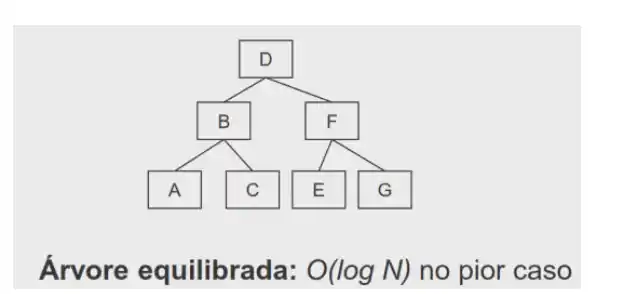
# Complexidade das operações
Proporcional ao número de Nodos por onde passamos.
Ou O(log N)

Se queremos uma arvore equilibrada as operações são sempre O(log N)

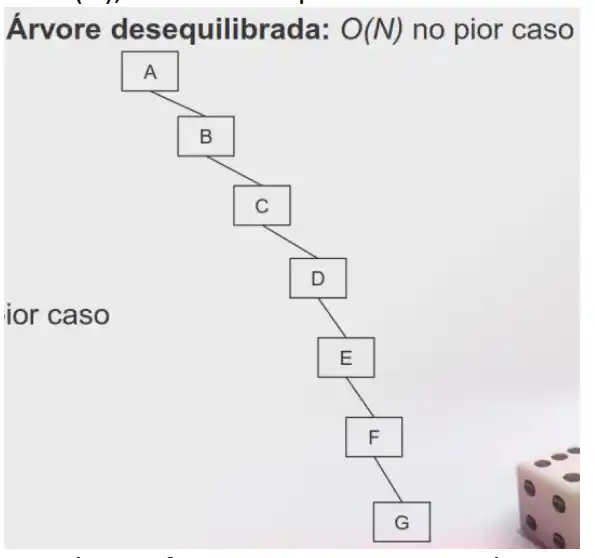
Ou O(N), árvore desequilibrada

Esta árvore ficou assim porque os valores estão de forma crescente
E será um cenário comum? Sim infelizmente, a árvore binária então comporta-se mal
O principal problema reside no facto de a introdução de sequências ordenadas (ou semiordenadas) é uma acção relativamente frequente,  resultando directamente na redução ao pior caso possível.

Relembrar que:
Operação constante

Uma operação é constante numa arvore só quando acedemos à raiz

#Propriedade de ordem (relembrar)
Faz com que a inserção e a procura de valores seja eficiente ou que seja simples, permite fazer
um percurso direto da raiz até aos valores que pretendo

#Propriedade de equilíbrio
Para além da propriedade de ordem, pode ser também adicionada uma propriedade adicional
que assegura o equilíbrio da árvore.
Nenhum nodo poderá atingir uma profundidade demasiado elevada em relação aos outros.
Há diferentes variantes da propriedade de equilíbrio (por esta via surgem as arvores binárias
auto balanceadas).
As operações de inserção e remoção tornam-se mais complicadas, mas a operação de pesquisa
fica mais eficiente.

Existem várias propriedades de equilibro, sendo que:
A propriedade de equilíbrio mais simples é requerer que as subárvores direita e esquerda
tenham a mesma profundidade se possível. Esta abordagem pode implicar modificar todos os
Nodos da arvore, o que implica demorar muito e complicado de ser feito.

Surge então a propriedade de equilíbrio AVL. Para qualquer nodo na árvore, a profundidade
das subárvores direita e esquerda só pode diferir em 1 (a profundidade de uma subárvore
vazia é -1).

No AVL:

Profundidade do lado esquerdo de E é 3
Profundidade do lado direito de E é 2
3-2=1, esta equilibrado

Profundidade do lado esquerdo de C é 2
Profundidade do lado direito de C é 1
2-1=1, esta equilibrado

Profundidade do lado esquerdo de G é 1
Profundidade do lado direito de C é 0
1-0=1, esta equilibrado

Todos os nós estão equilibrados.

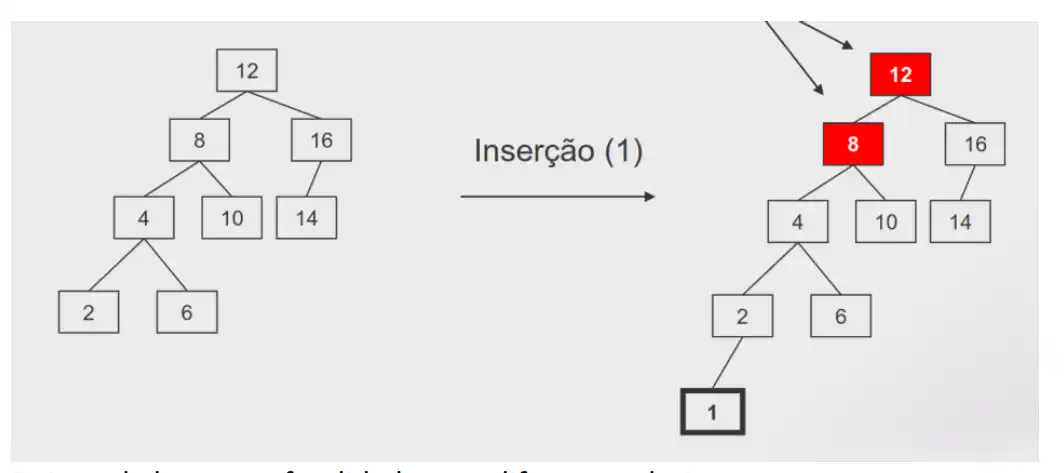
Exemplo: inserir o 1

Deixou de haver profundidade com diferenças de 1

Depois da inserção, torna-se necessário efetuar uma operação adicional que assegura a
preservação equilíbrio da árvore.

Os desequilíbrios (que surge do percurso que foi feito até chegar ao nó desequilibrado) podem resultar dos cenários:
Ou

E vai ser uma inserção externa
O resultado de uma inserção exterior pode ser equilibrado com uma única rotação da árvore.
Ou

E vai ser uma inserção interna
O resultado de uma inserção interior pode ser equilibrado com duas rotações da árvore.

Face à inserção externa a rotação é feita entre o Nodo e o seu descendente
O nodo X1 sobe e o nodo X2 desce

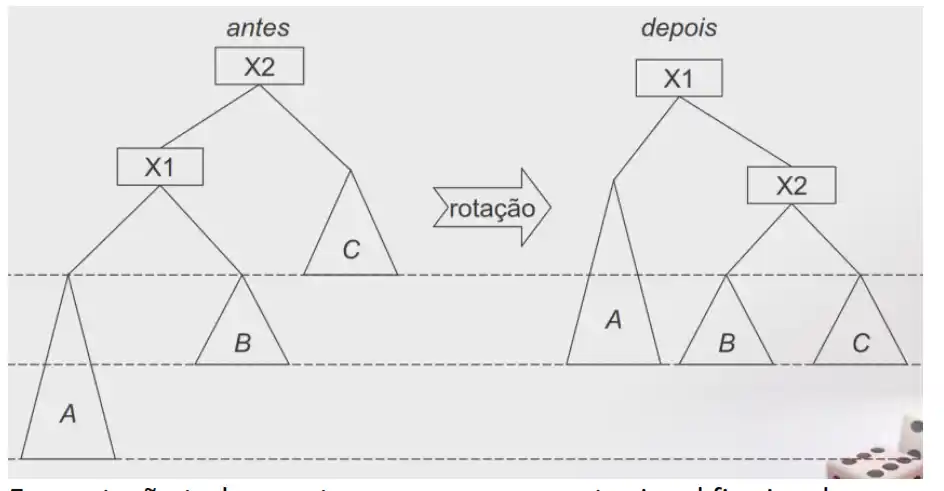
E na rotação tudo o resto que se possa manter igual fica igual

pag38